VMLS 12.1 最小二乗法 その一

線形代数

こんにちは。ごるごです。

研究室の宿題で線形代数を勉強しなければならないので、ついでにこのブログで勉強の記録も付けていきたいと思います。テキストはこちらになります。

web.stanford.edu

基本的にはテキストをざっくりと翻訳していく形になるかと思います。ところどころ日本語があやしい箇所がありますがご容赦ください(できればコメントで添削してほしい)。また、諸事情によりChapter 12のLeast Squaresから始めます。

それでは、スタート

Chapter 12 Least squares

　この章では、連立一次方程式の誤差の二乗和を最小化することで、over-determined*1 な連立方程式の近似解を求める強力な手法を学ぶ。その手法と、後の章で記載されるいくつかの拡張は幅広い分野に応用されている。最小二乗法は19世紀にガウスとルジャンドル二人の数学者によって独立に発見された。

12.1 Least squares problem

　{\displaystyle m\times n} 型の係数行列 {\displaystyle A} が縦長であるとき、連立方程式は { \displaystyle Ax=b } と表され、{\displaystyle b} が {\displaystyle m} 次元ベクトルであるので、この連立方程式は over-determined となる。すなわち、方程式の数 {\displaystyle m} が選択できる変数の数 {\displaystyle n} よりも多い。これらの方程式は、{\displaystyle b} が {\displaystyle A} の各列の線形結合であるときのみ解をもつ。
　しかし、ほとんどの {\displaystyle b} において、{ \displaystyle Ax=b } を満たす {\displaystyle n} 次元ベクトル {\displaystyle x} は存在しない。妥協案として、我々は残差　{ \displaystyle r=Ax-b } を最小化する {\displaystyle x} を探すことにする。つまり、残差のノルム { \displaystyle ||Ax-b|| } を最小化するということである。もし残差ベクトルが小さくなるなら、{ \displaystyle Ax\approx b } であると言える(いくつかの本では残差は { \displaystyle b-Ax } と定義されるが、{ \displaystyle ||Ax-b||=||b-Ax|| } であるため差し支えない)。
　残差のノルムを最小化することと残差の二乗を最小化することは同義であるため、

{ \displaystyle \begin{equation}||Ax-b||^2=||r||^2=r_1^2+\cdots+r_m^2\end{equation} }
により残差の二乗和を最小化できる。すべての可能な {\displaystyle x} から { \displaystyle ||Ax-b||^2 } を最小化する {\displaystyle n} 次元ベクトル { \displaystyle \hat{x} } を求める問題を、最小二乗法(least squares problem)という。最小二乗法は次のような表記
{ \displaystyle minimize\quad ||Ax-b||^2\qquad (12.1) }
により表され、(12.1)はこれを満たす {\displaystyle x} を求めることを意味する。行列 {\displaystyle A} とベクトル {\displaystyle b} を(12.1)のデータと呼ぶ。最小化される量 { \displaystyle ||Ax-b||^2 } を、最小二乗法(12.1)の目的関数(objective function)という。(12.1)は線形最小二乗法(linear least squares)と呼ばれることがある。残差 {\displaystyle r} が {\displaystyle x} のアフィン変換であることを強調したい場合や、残差 {\displaystyle r} が {\displaystyle x} の任意の関数である非線形最小二乗法と区別したい場合に用いられる。
　すべての {\displaystyle x} で { \displaystyle ||A\hat{x}-b||^2\leq||Ax-b||^2 } を満たすどのようなベクトル {\displaystyle \hat{x}} も最小二乗法(12.1)の解である。そのようなベクトルを { \displaystyle ||Ax-b||^2 } の最小二乗解(least squares approximate solution)と呼ぶ。ここで、{ \displaystyle Ax=b } の近似解 {\displaystyle \hat{x}} が { \displaystyle A\hat{x}=b } を満たさないことに注意する。{\displaystyle \hat{x}} は単に残差のノルムを最小化したものにすぎない。「{\displaystyle \hat{x}} は { \displaystyle Ax=b } の最小二乗法的に解く」などという紛らわしい説明を使う本もあるが、一般的に、最小二乗解 {\displaystyle \hat{x}} は等式 { \displaystyle Ax=b } を解けないことを強調しておく。
　(我々が元々の残差のノルムと呼ぶところの) { \displaystyle ||Ax-b||^2 } が小さいとき、{\displaystyle \hat{x}} は { \displaystyle Ax=b } を近似的に解けると言える。つまり、もしもある  { \displaystyle n } 次元ベクトル  { \displaystyle x } が  { \displaystyle Ax=b } を満足するならば、残差のノルムはゼロであり、最小二乗解となる。
　データフィッティングへの応用(次章のトピックである)で典型的に用いられる最小二乗法(12.1)の他の名称は回帰(regression)である。最小二乗解 {\displaystyle \hat{x}} はベクトル {\displaystyle b} を {\displaystyle A} の各列に回帰させた結果である。

列の解釈

{\displaystyle A} の各列が {\displaystyle m} 次のベクトルであるとき、最小二乗法(12.1)は {\displaystyle m} 次ベクトル {\displaystyle b} に最も近い各列の線形結合を求める問題となる。つまり、ベクトル {\displaystyle x} は係数を与える。

{ \displaystyle ||Ax-b||^2=||(x_1 a_1 +\cdots+x_n a_n)-b||^2. }
{\displaystyle \hat{x}} が最小二乗解であるとき、ベクトル
{ \displaystyle A\hat{x}=\hat{x}_1 a_1+\cdots+\hat{x}_n a_n}
は、すべてのベクトル { \displaystyle a_1,...,a_n } の線形結合の中で、最もベクトル { \displaystyle b } に近づく。

行の解釈

{ \displaystyle A} の各行が { \displaystyle n} 次の行ベクトル { \displaystyle \tilde{a}^T_1,...,\tilde{a}^T_n } であるとすると、残差の成分は次のように与えられる。

{ \displaystyle r_i=\tilde{a}^T_i x-b_i,\quad i=1,...,m. }
最小二乗法の目的関数は
{ \displaystyle ||Ax-b||^2=(\tilde{a}^T_1 x-b_1)^2+\cdots+(\tilde{a}^T_m x-b_m)^2, }

つまり、{ \displaystyle m} 本のスカラーの連立一次方程式における残差の二乗和である。我々の目的がすべての残差を小さくする { \displaystyle x} を選ぶことであるならば、この残差の二乗和を最小化することは道理にかなった解釈である。

Example

次のようなデータをもつ最小二乗法を考える。

{ \displaystyle \begin{bmatrix} 2&0\\-1&1\\0&2 \end{bmatrix} ,\quad \begin{bmatrix} 1\\0\\-1\end{bmatrix}. }
{ \displaystyle Ax=b} の二変数に対して over-determined な三本の方程式の組
{ \displaystyle 2x_1=1,\quad -x_1+x_2=0,\quad 2x_2=-1}
は解を持たない(一つ目の方程式からは { \displaystyle x_1=1/2}、三つ目の方程式からは { \displaystyle x_2=-1/2} が得られるが、二つ目の方程式を満たさない)。相当する最小二乗法は
{ \displaystyle minimize\quad (2x_1-1)^2+(-x_1+x_2)^2+(2x_2+1)^2 }
である。この最小二乗法は次章で紹介する手法を用いることで解ける(または、単純に計算する)。その唯一の解は {\displaystyle \hat{x}=(1/3,-1/3) } である。最小二乗法解 {\displaystyle \hat{x} } は等式 {\displaystyle Ax=b } を満たさない。その残差は
{\displaystyle \hat{r}=A\hat{x}-b=(-1/3,-2/3,1/3) }
であり、二乗和は {\displaystyle ||A\hat{x}-b||^2=2/3 } である。この近似解と、先ほどの {\displaystyle Ax=b } の一つ目と二つ目の方程式の(厳密な)解である {\displaystyle \hat{x}=(1/2,-1/2) } とを比較してみる。残差は
{\displaystyle \hat{r}=A\hat{x}-b=(0,-1,0) }
であり、二乗和は {\displaystyle ||A\hat{x}-b||^2=1 } である。
　行の解釈は我々に
{ \displaystyle (1/3)\begin{bmatrix} 2\\-1\\0 \end{bmatrix} +(-1/3) \begin{bmatrix} 0\\1\\2 \end{bmatrix}=\begin{bmatrix} 2/3\\-2/3\\-2/3 \end{bmatrix} }
が {\displaystyle b } に最も近い {\displaystyle A } の各行の線形結合であることを教えてくれる。
　図 12.1 は {\displaystyle x=(x_1,x_2) } に対する目的関数 {\displaystyle ||A\hat{x}-b||^2 } の値を示している。また、{\displaystyle ||A\hat{x}-b||^2=2/3 } のときの最小二乗解 {\displaystyle \hat{x} } 黒点で示している。曲線は目的関数の値が {\displaystyle ||A\hat{x}-b||^2+1, ||A\hat{x}-b||^2+2, \cdots } の場合の点 {\displaystyle x } を表している。
Introduction to Applied Linear Algebra – Vectors, Matrices, and Least Squares

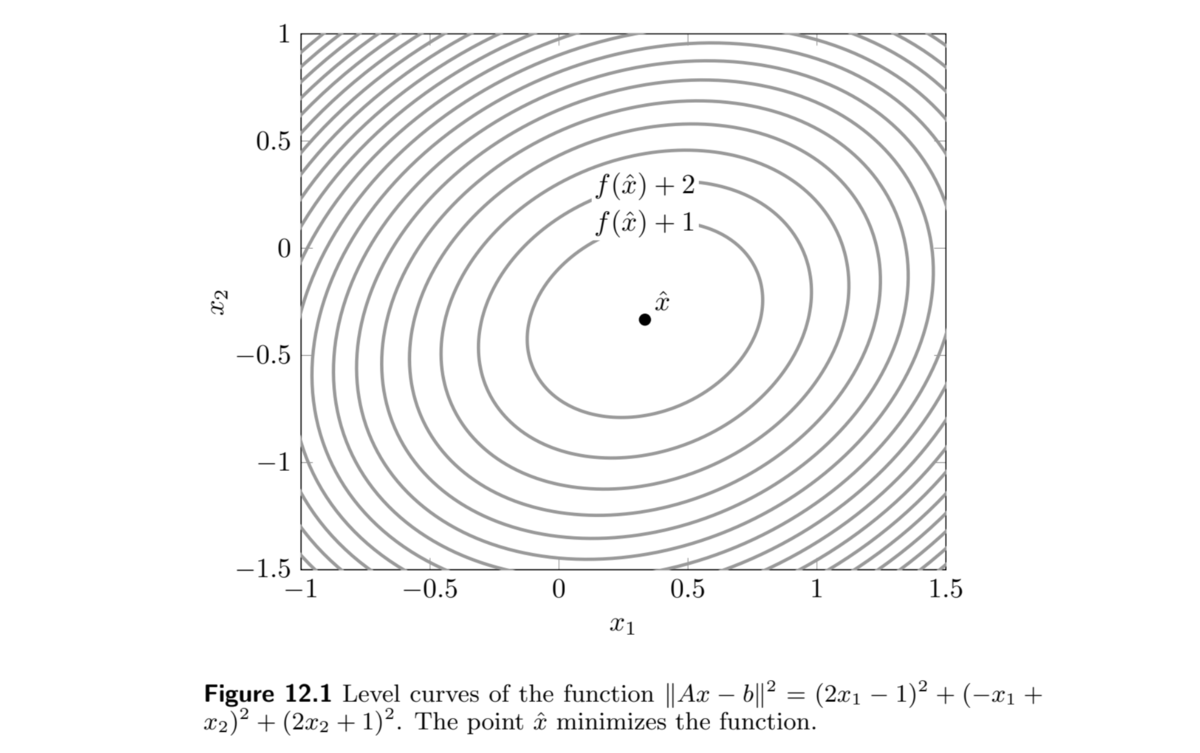
次回→VMLS 12.2

*1:Over-determinedとは、連立一次方程式において方程式の数が未知数の数より多い状態のこと。これは、連立方程式を { \displaystyle Ax=b } のような行列表示で表したとき、係数行列 {\displaystyle A} が縦長の行列であることを意味する。Over-determined な連立方程式は解が係数行列の線形結合で表される場合を除き解くことができない。